Risk analysis

Analyzing risks

In this perspective, various privacy risks can be analyzed. These include re-identification risks for the prosecutor, journalist and marketer attacker models as well as risks derived from population uniqueness, which can be estimated with different statistical methods. Moreover, the perspective provides methods for detecting HIPAA identifiers in the dataset and for finding further quasi-identifiers.

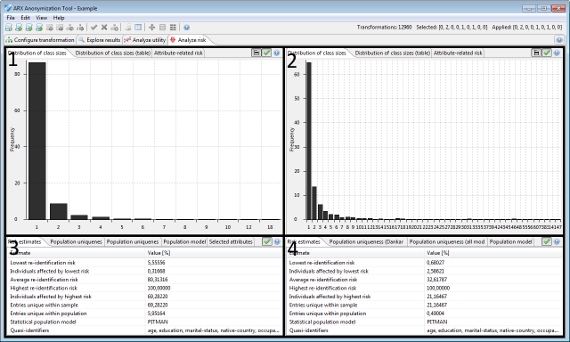
Distribution of risks

In this view, the distribution of re-identification risks amongst the records of the dataset is displayed. The distribution is calculated for both input and output data, either as a histogram or as a table.

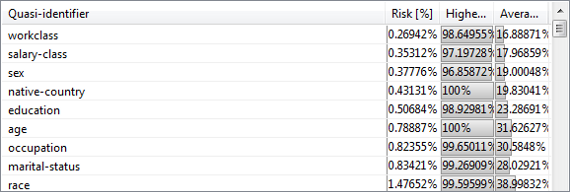
Finding quasi-identifiers

In this view, combinations of attributes can be analyzed regarding associated risks of re-identification. The view provides information about the degree to which combinations of variables separate the records from each other and to which degree the variables make records distinct. First, a set of attributes must be selected for further analysis in the bottom left area.

ARX will then calculate the aforementioned parameters.

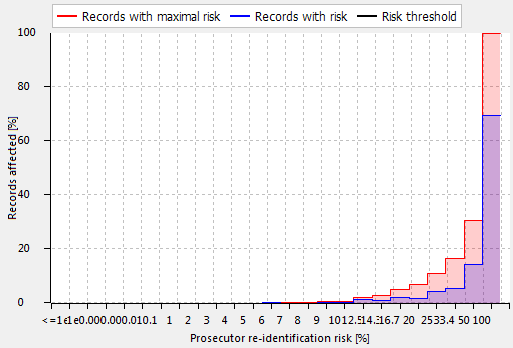
Re-identification risks

This view displays an overview of several measures for re-identification risks. In the upper area of this perspective, risk estimates are provided for three different attacker models: (1) the prosecutor scenario, (2) the journalist scenario and (3) the marketer scenario.

Thresholds can be provided for the highest risk of any record, for the records that have a risk higher than this threshold and for the average fraction of records that can successfully be re-identified. More details about the methods can be found in the book Guide to the anonymization of Personal Health Information by Khaled el Emam.

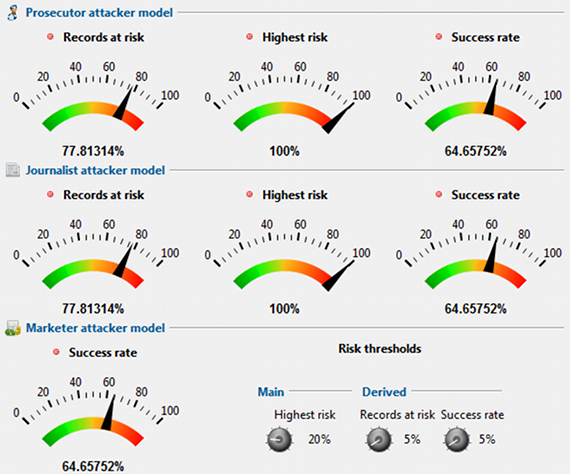
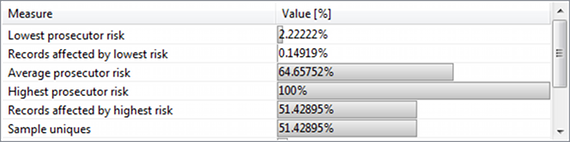
In the lower part of the perspective, selected measures of prosecutor re-identification risks are displayed. These measures are based on the sample itself. They are complemented by numbers on population uniqueness from a selected statistical model:

• Lowest prosecutor re-identification risk.
• Individuals affected by lowest risk.
• Highest prosecutor re-identification risk.
• Individuals affected by highest risk.
• Average prosecutor re-identification risk.
• Fraction of unique records.

HIPAA identifiers

The Safe Harbor method of the US Health Insurance and Portability and Accountability Act specifies 18 identifiers that must be modified or removed in order to derive a de-identified dataset. The aim of this perspective is to detect such identifiers.

Note: This method works on a best-effort basis. If no HIPAA identifiers are detected, this does not mean that no HIPAA identifiers are present. ARX favors recall over precision and it does not implement methods for detecting all types of HIPAA identifiers. The following types of attributes specified by HIPAA can potentially be detected:

• Names,
• Geographical subdivisions: regions, states, cities,
• Dates,
• Phone numbers,
• Fax numbers,
• Electronic mail addresses,
• Social Security numbers,
• License plate numbers,
• Universal Resource Locators (URLs),
• Internet Protocol (IP) addresses.

The method computes edit distances between common labels for HIPAA identifiers and the labels of the attributes in the dataset. Moreover, it checks the values of the attributes for common patterns (e.g. of license plate numbers, ZIP codes and dates) and common instance values (e.g. first names and last names).

Population uniqueness

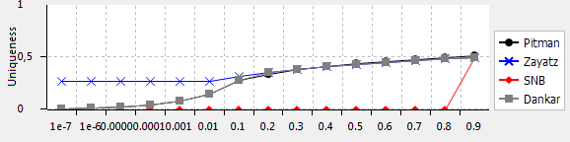
ARX supports the estimation of re-identification risks based on the number of population uniques in a sample. Population uniques are records that are unique within the sample (sample uniques) and which are also unique within the underlying population from which the data has been samples. Note: Not all sample uniques are also population uniques. When no data about the population has been loaded into ARX in the form of a population table, this number can be estimated with statistical models. Super-population models estimate the characteristics of the overall population with probability distributions that are parameterized with sample characteristics. ARX supports the methods by Hoshino (Pitman), Zayatz and Chen and McNulty (SNB).

Different models may return differently accurate estimates of the number of population uniques. As a rule of thumb, the Pitman model should be used for sampling fractions lower than or equal to 10%. ARX also implements a decision rule proposed and validated for clinical datasets by Dankar et al. More information can be found here.

The tool also provides a view for comparing the results of different methods under the assumption of different sampling fractions:

In the process of computing estimates with statistical models ARX must solve non-linear bivariate equation systems. The solver used by ARX can be configured in the settings dialog. Here, you may specify options such as the total number of iterations, iterations per try and the required accuracy etc. Changing these settings may influence the precision of the results and the time required to obtain them.

Note: Methods for estimating population uniqueness assume that the dataset is a uniform sample of the population. If this is not the case, results may be inaccurate.

Population settings

Methods for estimating the number of population uniques in a dataset require some basic data about the population from which the dataset was sampled. ARX provides default settings for populations, such as the USA, UK, France or Germany, which can be selected in the following area in the configuration perspective:

It is important that the underlying population matches the population that the anticipated adversary is likely to know that the data has been sampled from. If the required data is not provided by ARX, it can also be entered manually.

Note: Methods for estimating population uniqueness assume that the dataset is a uniform sample of the population. If this is not the case, results may be inaccurate.