1. Introduction
2. Defining input data
3. Generalization
4. Adding a generalization hierarchy to the data definition
5. Defining privacy models and transformation rules
6. Executing the anonymization algorithm
7. Accessing and comparing data
8. Analyzing re-identification risks
9. Writing data
Please note: the documentation provided on this page is currently (as of March 2018) quite outdated. ARX is developed with backwards-compatibility in mind, so it is expected that the examples included here will still work with the current version. However, a lot of functionality has been added in the meantime, which is not, yet, documented here.
All features that are accessible via the graphical interface are also accessible via the public API. However, the aim of the programming interface is to provide de-identification methods to other software systems and we note that interaction with the software library provided by ARX will often be simpler than interaction with the graphical tool. Programmatic access will usually rely on ARX’s ability to automatically determine a solution to a privacy problem.
1. Introduction
This document provides a brief overview over the ARX API. It covers loading data, defining data transformations, altering and manipulating data and processing the results of the algorithm. More detailed examples are provided in the “examples” package. A Javadoc documentation is available in the “doc” folder.
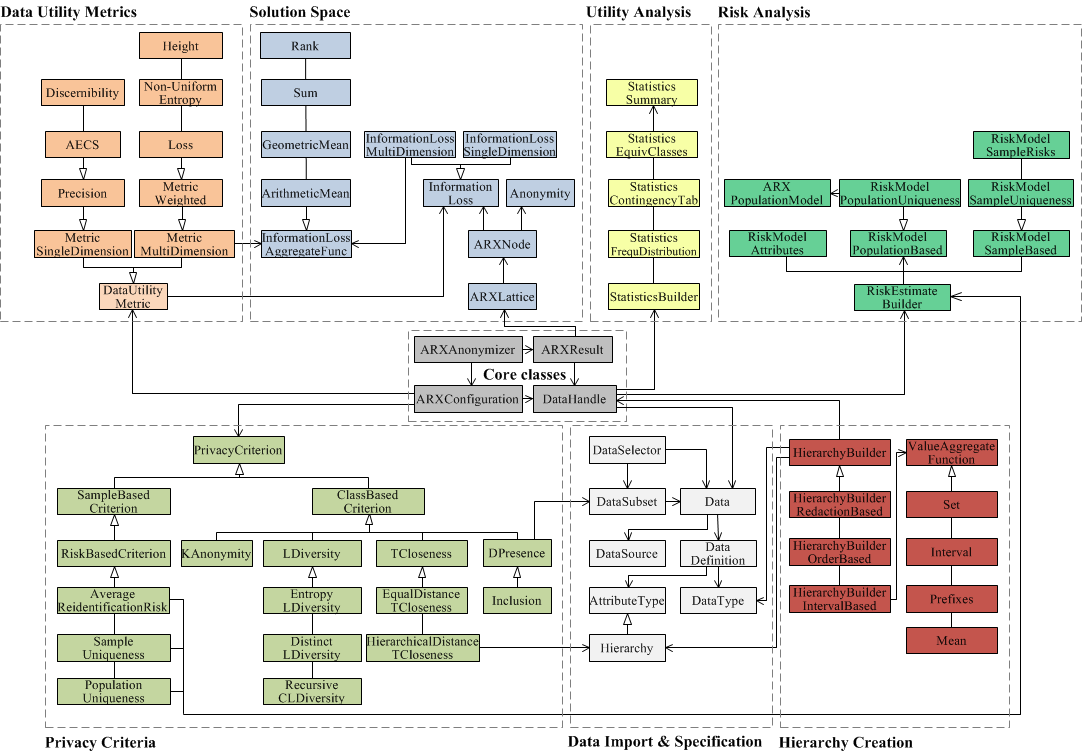
A Unified Modeling Language (UML) diagram of the most important classes of our API is shown in the above Figure. It can be seen that the API consists of a set of packages for 1) data import and specification, 2) hierarchy generation, 3) privacy models, 4) measuring data utility, 5) utility analysis, 6) representing the solution space, and, 7) risk analyses. The classes ARXConfiguration, ARXAnonymizer and ARXResult provide the main interfaces to ARX’s functionalities. Data and attribute types are provided as static variables from the DataType and AttributeType classes respectively. The class DataHandle allows users to interact with the data (read-only), by performing operations such as sorting, swapping rows or reading cell values. Handles can be obtained for input data, output data and research subsets of such data. Data handles representing input and derived output data are linked with each other, meaning that operations performed on one representation are transparently performed on all other representations as well. For example, sorting the input data sorts the output data analogously. The class ARXLattice offers several methods for exploring the solution space and for obtaining information about the properties of transformations (represented by the class ARXNode). The class Inclusion implements a dummy privacy models that can be used to exclude records from the input dataset by defining a research subset.
2. Loading and specifying data
The class Data offers different means to provide data to the ARX framework. This currently includes loading data from a CSV file, or reading data from input streams, iterators, lists or arrays:
Data data = Data.create("data.csv", Charset.defaultCharset(), ';');
Defining data manually
DefaultData data = Data.create();
data.add("age", "gender", "zipcode");
data.add("34", "male", "81667");
Since ARX 2.1. data can also be imported from Excel files and relational database systems.
Accessing an Excel file
DataSource source = DataSource.createExcelSource("data/test.xls", 0, true);
source.addColumn(1, DataType.STRING);
source.addColumn("age", "renamed", DataType.INTEGER);
source.addColumn(2, DataType.STRING);
Columns are created in the order in which they are added to the source. Columns can be referenced by indexes or names. Moreover, data types can be defined. A similar mechanism is available for CSV files (DataSource.createCSVSource(…)) and relational databases (DataSource.createJDBCSource(…)).
Further methods
Data.create(File file, Charset charset, char separator); Data.create(InputStream stream, Charset charset, char separator); Data.create(Iterator<String[]> iterator); Data.create(List<String[]> list); Data.create(String[][] array);
Assigning data types
ARX implements five different data types that are available via the class DataType: ARXInteger, ARXDecimal, ARXDate, ARXOrderedString, ARXString. Decimals require a format string matching the format required by DecimalFormat and Dates require a format string matching to requirements of SimpleDateFormat.
Listing and instantiating available data types
DataType.list()
type.getLabel();
type.getWrappedClass();
type.hasFormat();
DataType<?> instance = type.newInstance();
if (type.hasFormat() && !type.getExampleFormats().isEmpty()) {
instance = type.newInstance(type.getExampleFormats().iterator().next());
}
DataTypeDescription<Double> entry = DataType.list(Double.class);
3. Generalization
In terms of attribute types, the transformation can be defined via the DataDefinition object, which can be retrieved for a Data object by calling data.getDefinition(). The framework distinguishes between four different kinds of attributes, which are encapsulated in the class AttributeType. Insensitive attributes will be kept as is, directly-identifying attributes will be removed from the dataset, quasi-identifying attributes will be transformed by applying the provided generalization hierarchies and sensitive attributes will be kept as is and can be utilized to generate l-diverse or t-close transformations.
Defining attribute types
data.getDefinition().setAttributeType("age", AttributeType.IDENTIFYING_ATTRIBUTE);
data.getDefinition().setAttributeType("gender", AttributeType.SENSITIVE_ATTRIBUTE);
data.getDefinition().setAttributeType("zipcode", AttributeType.INSENSITIVE_ATTRIBUTE);
Generalization hierarchies extend the class AttributeType and can therefore be assigned in the same way as the other types of attributes. Generalization hierarchies can be defined in the same way as Data objects.
Manually defining a generalization hierarchy
DefaultHierarchy hierarchy = Hierarchy.create();
hierarchy.add("81667", "8166*", "816**", "81***", "8****", "*****");
hierarchy.add("81675", "8167*", "816**", "81***", "8****", "*****");
Loading a hierarchy from a file
Hierarchy hierarchy = Hierarchy.create("hierarchy.csv", ';');
Further methods
Hierarchy.create(File file, char separator); Hierarchy.create(InputStream stream, char separator); Hierarchy.create(Iterator<String[]> iterator); Hierarchy.create(List<String[]> list); Hierarchy.create(String[][] array);
Creating functional hierarches
The following example defines an interval-based hierarchy for LDL cholesterol:
// Create the builder HierarchyBuilderIntervalBased<Double> builder = HierarchyBuilderIntervalBased.create(DataType.DECIMAL); // Define base intervals builder.addInterval(0d, 1.8d, "very low"); builder.addInterval(1.8d, 2.6d, "low"); builder.addInterval(2.6d, 3.4d, "normal"); builder.addInterval(3.4d, 4.1d, "borderline high"); builder.addInterval(4.1d, 4.9d, "high"); builder.addInterval(4.9d, 10d, "very high"); // Define groups builder.getLevel(0).addGroup(2, "low").addGroup(2, "normal").addGroup(2, "high"); builder.getLevel(1).addGroup(2, "low-normal").addGroup(1, "high");
Loading/saving hierarchy specifications
builder.save("test.ahs");
HierarchyBuilder<?> builder = HierarchyBuilder.create("test.ahs");
if (builder.getType() == Type.REDACTION_BASED) {
(HierarchyBuilderRedactionBased)builder;
}
4. Adding a generalization hierarchy to the data definition
data.getDefinition().setAttributeType("zipcode", hierarchy);
There are further properties that can be set via the class DataDefinition. This includes the minimum and maximum levels of generalization that should be applied for a quasi-identifier. For example, it can be stated that a quasi-identifier should only be generalized to the levels 2-4 of its generalization hierarchy via:
data.getDefinition().setMinimumGeneralization("age", 2);
data.getDefinition().setMaximumGeneralization("age", 4);
Note: These properties are optional. Per default the anonymizer completely leverages the available generalization hierarchies.
The class DataDefinition also provides means to specify data types for each column. These data types are encapsulated in the class DataType. Currently “String”, “Decimal” and “Date” are implemented. The data types are used for sorting the data accordingly (see section 5). All transformed data is automatically treated as a string in the representation of the output data, as it is very unlikely that there is a generalization of a decimal or date that will preserve the data type (e.g, “8881″ -> “88″).
data.getDefinition().setDataType("age", DataType.DECIMAL);
data.getDefinition().setDataType("date-of-birth", DataType.DATE("dd.mm.yyyy"));
data.getDefinition().setDataType("city", DataType.STRING);
Note: There is no need to specify a data type. Per default everything is treated as a string. Defining a datatype will yield a more natural order when sorting data, though (see section 5).
The class DataDefinition also provides means to access information about the defined data transformation, such as the types of attributes, the height of the generalization hierarchies etc.
5. Defining privacy models and transformation rules
All further parameters of the anonymization algorithm are defined in an instance of the class ARXConfiguration. This includes parameters such as the suppression limit and the privacy models that should be used. The following example uses k-anonymity and a 2% suppression limit:
ARXConfiguration config = ARXConfiguration.create(); config.addPrivacyModel(new KAnonymity(5)); config.setSuppressionLimit(0.02d);
Privacy models that protect data from attribute disclosure, must be assigned to a sensitive attribute:
// Define sensitive attribute
data.getDefinition().setAttributeType("disease", AttributeType.SENSITIVE_ATTRIBUTE);
// t-closeness
config.addPrivacyModel(new HierarchicalDistanceTCloseness("disease", 0.2d, Hierarchy.create("disease.csv")));
config.addPrivacyModel(new EqualDistanceTCloseness("disease", 0.2d));
// l-diversity
config.addPrivacyModel(new DistinctLDiversity("disease", 2));
config.addPrivacyModel(new EntropyLDiversity("disease", 2));
config.addPrivacyModel(new RecursiveCLDiversity(3, 2, "disease"));
// δ-presence
config.addPrivacyModel(new DPresence(0.5, 0.66, subset));
// Statistical models
config.addPrivacyModel(new AverageReidentificationRisk(0.01d));
config.addPrivacyModel(new SampleUniqueness(0.01d));
config.addPrivacyModel(new PopulationUniqueness(0.01d, PopulationUniquenessModel.DANKAR,
ARXPopulationModel.create(Region.USA)));
// Include/exclude records from the dataset
config.addPrivacyModel(new Inclusion(subset));
For risk-based models that use population uniqueness, multiple statistical models may be used
PopulationUniquenessModel.DANKAR PopulationUniquenessModel.PITMAN PopulationUniquenessModel.ZAYATZ PopulationUniquenessModel.SNB
The underlying population must be specified. Several default instances exist, e.g.:
ARXPopulationModel.create(Region.USA); ARXPopulationModel.create(Region.UK); ARXPopulationModel.create(Region.FRANCE); ARXPopulationModel.create(Region.GERMANY);
Risk-based anonymization with super-population models requires solving non-linear bivariate equation systems. The solver used by ARX can be configured:
ARXSolverConfiguration.create().accuracy(1e-9) .iterationsPerTry(100) .iterationsTotal(1000) .timePerTry(10) .timeTotal(100);
For enforcing δ-presence, a research subset must be defined. This can be implemented with three different mechanisms. Firstly, the research subset can be defined explicitly and matched against the overall dataset:
Data data = Data.create("input.csv", ';');
Data subset = Data.create("subset.csv", ';');
DataSubset subset = DataSubset.create(data, subset);
Secondly, the subset can be specified by selecting rows from the input dataset:
DataSelector selector = DataSelector.create(data).field("age").leq(30);
DataSubset subset = DataSubset.create(data, selector);
Thirdly, the subset can be specified as a set of row indices:
Integer rows = new HashSet<integer>(); rows.add(1); rows.add(2); DataSubset subset = DataSubset.create(data, rows);
The resulting subset can be used to create an instance of the δ-presence model as follows:
DPresence d = new DPresence(0.5, 0.66, subset);
Furthermore, it is possible to specify the metric that is to be used for measuring information loss. The ARX framework currently supports the following metrics, which are derived from the class Metric:
config.setQualityModel(Metric.createEntropyMetric()); config.setQualityModel(Metric.createNMEntropyMetric()); config.setQualityModel(Metric.createDMStarMetric()); config.setQualityModel(Metric.createPrecisionMetric()); config.setQualityModel(Metric.createHeightMetric()); config.setQualityModel(Metric.createAECSMetric());
Algorithm-specific parameters such as the snapshot size or the maximum size of the history, which are only performance-related and will not influence the actual result, can be defined in an instance of the class ARXAnonymizer. Moreover, the string that should be inserted for suppressed values can be specified:
ARXAnonymizer anonymizer = new ARXAnonymizer();
anonymizer.setSuppressionString("*");
anonymizer.setMaximumSnapshotSizeDataset(0.2);
anonymizer.setMaximumSnapshotSizeSnapshot(0.2);
anonymizer.setHistorySize(200);
anonymizer.setRemoveOutliers(true);
6. Executing the anonymization algorithm
For a given Data object, the algorithms can be executed by calling:
ARXResult result = anonymizer.anonymize(data, configuration);
The method returns an instance of the class ARXResult. This class provides means to access the generalization lattice, which has been searched by the algorithm. Furthermore, it returns whether an anonymous transformation has been found, and provides access to the transformation with minimal information loss. Each transformation in the search space is represented by an instance of the class ARXNode. It provides to access the following information:
ARXNode node = result.getOptimalTransformation(); // Lower bound for the information loss node.getMinimumInformationLoss(); // Upper bound for the information loss node.getMaximumInformationLoss(); // Predecessors node.getPredecessors(); // Successors node.getSuccessors(); // Returns whether the transformation fulfills all privacy models node.isAnonymous() // Generalization defined for the given quasi identifier node.getGeneralization(String attribute)
Lower and upper bounds for information loss are provided because the ARX framework will not compute the information loss for all nodes, as it prunes parts of the search space. If a node has not been checked explicitly, its information loss will be between the returned boundaries. A transformation which has been checked explicitly (which will always be true for the global optimum) will return the same values for the lower and the upper bound.
7. Accessing and comparing data
The ARX framework provides a convenient API for accessing the data in its original form and in a transformed representation. All data access is encapsulated in the abstract class DataHandle. A data handle for the original data can be obtained by calling Data.getHandle(), for globally optimal transformation it can be obtained via ARXResult.getHandle(), and for any other transformation by ARXResult.getHandle(ARXNode). If a research subset was defined, a view on any DataHandle can be created that only shows the rows contained in the subset:
DataHandle handle = ARXResult.getHandle(); DataHandle view = handle.getView();
The handles for the input and output data, as well as for the data subsets, are linked with each other, meaning that all operations performed on one of the representations will also be performed on the other representation. This includes sorting the data or swapping rows. Additionally, the data behind a DataHandle is dictionary compressed, resulting in a low memory footprint.
DataHandles are especially useful for graphical tools, because they can be utilized to compare data, while making sure that their representations are always in sync (i.e., the i-th row of the output dataset represents the transformation of the i-th row in the input dataset).
Since ARX 2.1., multiple output representations of a DataHandle can be mananged simultaneously.
Obtaining multiple handles
DataHandle optimal = result.getOutput(); DataHandle top = result.getOutput(lattice.getTop()); DataHandle bottom = result.getOutput(lattice.getBottom());
Please note that, if multiple output handles are created, they must be released manually to free the associated resources. If only one output representation is needed at a time, this is not necessary. A handle can be released using the following method:
handle.release();
Important methods
handle.getNumRows(); handle.getNumColumns(); handle.getValue(int row, int column); handle.sort(); handle.swap(int row1, int row2); handle.getAttributeName(int column);
Note that the data handles do only represent the actual datasets and do not include any information about the attribute types or generalization hierarchies. A data handle for the input dataset can therefore be obtained at any time. It will remain valid, even when the DataDefinition is altered in subsequent steps.
Data properties
With the following code you may compute the frequency distribution of the values of an attribute in a DataHandle:
handle.getStatistics().getFrequencyDistribution(0, true);
With the following code you can access information about the equivalence classes in a transformed dataset:
handle.getEquivalenceClassStatistics();
With the following code you can compute a contingency table of two attributes in a DataHandle:
data.getHandle().getStatistics().getContingencyTable(0, true, 2, true);
while (contingency.iterator.hasNext()) {
Entry e = contingency.iterator.next();
e.value1;
e.value2;
e.frequency;
}
With the following code you can access summary statistics:
data.getHandle().getStatistics().getSummaryStatistics(true);
8. Analyzing re-identification risks
ARX offers multiple methods for analyzing re-identification risks. You may analyze the risks associated with individual quasi-identifiers using the following mechanism:
// Define the population
ARXPopulationModel population = ARXPopulationModel.create(Region.USA);
// Analyze risks
RiskModelAttributes risks = handle.getRiskEstimator(population)
.getSampleBasedAttributeRisks();
// Print results
for (QuasiIdentifierRisk qi : risks.getAttributeRisks()) {
qi.getFractionOfUniqueTuples();
qi.getIdentifier();
}
You may also analyze the equivalence classes in a dataset:
// Define the population ARXPopulationModel population = ARXPopulationModel.create(Region.USA); // Analyze risks RiskModelHistogram classes = handle.getRiskEstimator(population) .getEquivalenceClassModel(); // Access results classes.getHistogram(); classes.getAvgClassSize(); classes.getNumClasses()
Or use risk measures derived from the distribution of the size of equivalence classes:
// Define the population ARXPopulationModel population = ARXPopulationModel.create(Region.USA); // Analyze risks RiskModelSampleRisks sampleRisks = handle.getRiskEstimator(population) .getSampleBasedReidentificationRisk(); // Access the results sampleRisks.getAverageRisk()); sampleRisks.getLowestRisk()); sampleRisks.getFractionOfTuplesAffectedByLowestRisk()); sampleRisks.getHighestRisk()); sampleRisks.getFractionOfTuplesAffectedByHighestRisk());
You may analyze sample uniqueness:
// Define the population ARXPopulationModel population = ARXPopulationModel.create(Region.USA); // Analyze risks RiskModelSampleUniqueness sampleUniqueness = handle.getRiskEstimator(population) .getSampleBasedUniquenessRisk(); // Access results sampleUniqueness.getFractionOfUniqueTuples()
Or population uniqueness estimated with super-population models:
// Define the population ARXPopulationModel population = ARXPopulationModel.create(Region.USA); // Analyze risks RiskModelPopulationUniqueness populationUniqueness = handle.getRiskEstimator(population) .getPopulationBasedUniquenessRisk(); // Access results populationUniqueness.getFractionOfUniqueTuples(PopulationUniquenessModel.ZAYATZ));
For this purpose, multiple stastical models may be used:
PopulationUniquenessModel.DANKAR PopulationUniquenessModel.PITMAN PopulationUniquenessModel.ZAYATZ PopulationUniquenessModel.SNB
The underlying population must be specified. Several default instances exist, e.g.:
ARXPopulationModel.create(Region.USA); ARXPopulationModel.create(Region.UK); ARXPopulationModel.create(Region.FRANCE); ARXPopulationModel.create(Region.GERMANY);
Using super-population models requires to solve non-linear bivariate equation systems. The solver used by ARX can be configured:
ARXSolverConfiguration.create().accuracy(1e-9) .iterationsPerTry(100) .iterationsTotal(1000) .timePerTry(10) .timeTotal(100);
9. Writing data
The classes DataHandle and Hierarchy provide methods to store them in a CSV representation:
Hierarchy/DataHandle.save(String path, char separator); Hierarchy/DataHandle.save(File file, char separator); Hierarchy/DataHandle.save(OutputStream out, char separator);