1. Introduction
2. Implementation details
3. Performance
1. Introduction
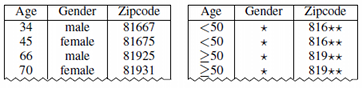
This project aims at providing a comprehensive, open source anonymization framework for (tabular) sensitive personal data using selected methods from the broad area of statistical disclosure control. The basic idea is to transform datasets in ways that make sure that they adhere to well-known formal privacy criteria. Typical examples include k-anonymity, l-diversity, t-closeness or δ-presence. The basic idea of k-anonymity is to protect a dataset against re-identification by generalizing the attributes which could be used in a linkage attack (quasi identifiers). A dataset is considered k-anonymous if each data item can not be distinguished from at least k-1 other data items. Further concepts help to prevent attribute disclosure (l-diversity), including background knowledge attacks (t-closeness), and prevents attackers from learning whether data about an individual is contained in the dataset (δ-presence). The following figure shows an example dataset with quasi identifiers “age”, “gender” and “zipcode” as well as a two-anonymous transformation:
Different types of algorithms can be used to transform datasets in such a way that they fulfill a given set of privacy criteria. For the biomedical domain, the use of globally-optimal anonymization algorithms that use multi-dimensional global recoding with full-domain generalization has been recommended. Globally-optimal anonymization means that a search space is constructed, from which the optimal solution is determined, i.e., a transformation resulting in minimal information loss regarding a given utility metric. Multi-dimensional global recoding means that the same generalization rules are applied to similar data entries, whereas full-domain generalization means that the entire domain of a data item is transformed to a more general domain (i.e., level) of its generalization hierarchy (see below). On the upside, this method results in datasets that are well suited for biomedical analyses and it provides a understandable process that can be configured by non-experts (e.g., by altering generalization hierarchies or choosing a suitable transformation from the solution space). On the downside, the underlying coding model is very strict and potentially results in low data quality. To prevent this, the method is often combined with local tuple suppression: outliers that violate the criteria are automatically removed from the dataset given that the total number of removed tuples is lower than a user-defined threshold. The following figure shows generalization hierarchies for the quasi identifiers in the example dataset:
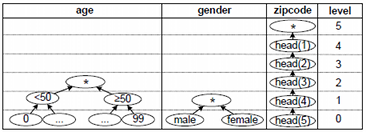
In the two-anonymous version of the dataset, the age is transformed to intervals of length 50 (level 1), the gender is suppressed (level 1) and the two least significant digits are dropped from the zipcode (level 2).
Similar to most algorithms for optimal k-anonymity, the ARX framework operates on a data structure called generalization lattice, which represents the search space and is shown in the following figure. An arrow denotes that a transformation is a direct generalization of a more specialized transformation and can be created by incrementing the generalization level of one of its predecessors’ quasi identifiers. The transformation with minimum generalization (0,0,0) is at the bottom and represents the original input dataset, whereas the transformation with maximal generalization (2,1,5) is at the top and represents (in this example) the complete suppression of all attribute values. The transformation that has been applied to anonymize the example dataset is (1,1,2).
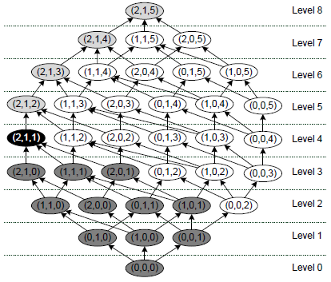
ARX further utilizes a common technique called predictive tagging. It requires the generalization hierarchies to be monotonic, which means that within one hierarchy the groups at level n+1 are defined by merging groups from level n. The monotonicity implies that all generalizations of an anonymous transformation are also anonymous and all specializations of a non-anonymous transformation are also not anonymous. This allows to prune large parts of the search space.
The monotonicity criterion for utility metrics requires that on each path from the bottom node to the top node of the generalization lattice, the measured information loss increases monotonically. This implies that if a generalization lattice is divided into a set of (potentially overlapping) paths the global optimum can be determined by only comparing the local optima. Furthermore, there is no need to evaluate data utility for transformations that have been tagged predictively, because they can never be a local or global optimum.
When anonymizing a dataset, algorithms for globally-optimal full-domain k-anonymity need to check a significant subset of all possible transformations for whether they result in an anonymized dataset. The ARX framework is therefore centered around a highly efficient implementation of this process. The groundwork is laid by a carefully engineered data encoding, representation and memory layout. Furthermore, ARX implements multiple generic optimizations that are enabled by interweaving the involved database operators with the anonymization algorithm.
2. Implementation details
The process of checking individual transformations for anonymity is the main bottleneck in many anonymization algorithms. The main design goal of the ARX framework is to speed up this process by choosing an appropriate encoding, data representation and memory layout. It further implements several optimizations enabled by these design decisions.
Data Representation
The framework holds all data in main memory. As the data is compressed and our optimizations are very efficient in terms of memory consumption this is feasible for datasets with up to several million data entries on current commodity hardware, depending on available main memory and dataset characteristics. The framework implements dictionary compression on all data items and represents generalization hierarchies in a tabular manner. The following figure shows an example encoding of the generalization hierarchy of the attribute “age” from the example:
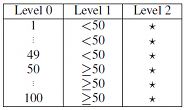
The framework utilizes one dictionary per attribute to map the values contained in the corresponding column onto integer values. By encoding the values from the input dataset before the values contained in the higher levels of the generalization hierarchies the framerwork ensures that the original values of a column with m distinct values get assigned the numbers 0 to m-1. This enables the efficient representation of the generalization hierarchies as two-dimensional arrays without wasting too much space, an example of which is shown in the following figure:
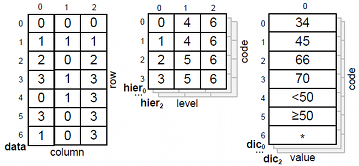
The values of the attribute age from column 0 and the relevant values from the generalization hierarchy are encoded in the corresponding dictionary dic[0]. The associated generalization hierarchy (hier[0]) is represented as a two dimensional array in which the i-th row contains the values for the original data item which is encoded as i in the dictionary. The j-th column stores the corresponding transformed value at the j-th level of the hierarchy. The other quasi-identifiers are handled analogously. The input dataset itself is represented as a row-oriented integer array (data). Additionally, the framework manages an analogous data structure, buffer, which is used to store a transformed representation of the original data. Based on this memory layout a transformation can be applied to the dataset without the need for complex join algorithms. Instead, transforming a value from the input data in cell (row, col) to the value defined on level level of its generalization hierarchy and storing it in the buffer can be implemented by a simple assignment:
buffer[row, col] = hier[col, data[row, col], level] (1)
Basic implementation
The basic implementation of a check for anonymity first transforms the input dataset by iterating over all rows in the buffer and applying the assignment (1) to each cell. Afterwards, each row is passed to a groupify operator which computes the equivalence classes. It is implemented as a hash table where each entry holds an associated counter, that is incremented whenever the same key (a row with identical cell values) is added. Finally, the framework iterates over all entries in the hash table and checks whether they fulfill the given set of privacy criteria. The ARX framework further allows a suppression parameter, that defines an upper bound for the number of rows that can be suppressed in order to still consider a dataset anonymized. This further reduces information loss as the privacy criteria are not enforced for all equivalence classes but non-anonymous groups are removed from the dataset as long as the total number of suppressed tuples is lower than the threshold. The framework provides several extensions that allow to find optimal solutions for privacy criteria which do not remain monotonic when implementing suppression, such as l-diversity.
Projection
Because ARX materializes the transformed data in a buffer it only needs to transform parts of the data that actually change. A projection can be applied if two consecutive transformations s1 and s2 define the same level of generalization for some quasi-identifiers. These columns are already represented correctly in the buffer and do not need to be transformed again. An example is shown in the following figure, where the columns 0 and 1 have already been processed as required when first checking the transformation (2,1,1) and then (2,1,3). Therefore only column 2 needs to be transformed:
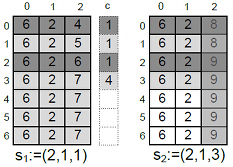
It is important to note that an efficient implementation of this optimization can not just iterate over the set of active columns when processing each row. The overhead induced by this additional indirection generally exceeds the positive effect of not having to transform some cells. The implementation is therefore based on branching into parameterized implementations for each possible number of active columns. E.g., the implementation that transforms two columns takes the arguments col1 and col2 and executes the following for each row in the dataset:
buffer[row, col1] = hier[col1, data[row, col1], level[col1]] buffer[row, col2] = hier[col2, data[row, col2], level[col2]]
Roll-Up
The roll-up optimization can be applied when the algorithm moves from a transformation s to a transformation s’, which is a generalization of s. The equivalence classes for s’ can then be built by merging the equivalence classes for s due to the monotonicity of the generalization hierarchies. The ARX framework implements this by storing the index of a representative tuple (the first row that has been added for an equivalence class) in each entry in the hash table and managing a second groupify operator. It then iterates over the hash table entries that have resulted from the previous check and transforms only the representative tuples. Because it uses an index into the original dataset instead of the actual equivalence classes, this only introduces a very small space overhead and the assignment (1) can again be applied instead of an actual join. The representative tuples are then passed to the second groupify operator together with the size of their original classes. The references to these two operators are exchanged prior to each check.
A roll-up is also possible in the transition shown in the figure above. Here, the groups are denoted by different shades of gray. Assuming that the previous transformation had to be checked by building equivalence classes over all rows, this resulted in the groups {0}, {1}, {2} and {3,4,5,6}. The representatives and sizes are (0,1), (1,1), (2,1) and (3,4) as indicated by the additional rightmost column. To compute the classes for s2 it is only necessary to process four rows, whereas seven rows had to be processed to check s1.
Maintaining a buffer of snapshots
A series of roll-up operations can only be performed on a path of non-anonymous transformations. A similar technique can be applied in other transitions if a buffer containing snapshots of the equivalence classes of previous transformations (called History) is managed. The classes represented by a transformation s can then be built by merging the classes defined by a snapshot of a more specialized transformation s’. If multiple suitable snapshots are available, the framework picks the one that contains the fewest classes. Due to the presence of pointers to representative rows in the groupify operators, the framework is able to only store references to the representative and the size for each equivalence class. This compact representation (8 bytes per class) allows to efficiently maintain a large number of snapshots. Furthermore, it is only necessary to store snapshots for non-anonymous transformations because otherwise all generalizations will never be checked but tagged predictively. A snapshot can also be pruned if all nodes that could possibly utilize it are already tagged. A simple check that covers parts of this restriction is to look at all direct generalizations of the state and discard the snapshot if these are all tagged as k-anonymous.
To further limit the memory consumption and prevent performance degradation, the framework introduces three parameters that control the buffer. The first parameter defines the maximum number of equivalence classes, relative to the number of data items in the original dataset, a snapshot is allowed to contain in order to be stored. The second parameter defines a relative reduction in size (number of equivalence classes) a snapshot has to provide in order to replace an existing snapshot in the history. The third parameter defines an upper bound for the number of entries that can be stored in the buffer at the same time. When this limit is reached, the framework first checks all contained snapshots for whether they can be dropped by looking at their direct generalizations. Otherwise, the least recently used snapshot is evicted. Buffering snapshots does not fully replace the roll-up optimization but complements it, as it only provides a limited number of snapshots of a predefined maximum size.
Putting it all together
When anonymizing a dataset, the framework combines all of the above optimizations. The example transition from the figure above can, e.g., benefit from performing a roll-up as well as a projection. In this particular case it is only necessary to transform one column for four representative rows, which results in four cells that need to be transformed. There are several limitations for valid combinations of optimizations that ensure that the data is always in a consistent state, though. Transitions are mainly restricted in the context of projections as these can only be performed successively if the current state allows to perform a roll-up or all rows have been transformed previously. The framework utilizes a finite state machine to comply with these restrictions.
Utility metrics are evaluated directly after checking a transformation for anonymity. Metrics that are based on the data itself or the resulting equivalence classes can then directly access the transformed data in the buffer or the entries in the hash table. All possibly optimal solution candidates are explicitly checked by the Flash Algorithm. If the metric is monotonic (e.g., DM*, Non-Uniform Entropy) the overall overhead for its evaluation is therefore very low because there is no need to evaluate it for transformations that have only been tagged.
3. Performance
The following figure shows the performance impact of the optimizations implemented by the ARX framework when k-anonymizing several real-world datasets, most of which have already been utilized for benchmarking previous work on data anonymization. The datasets include the 1994 US census database (ADULT), KDD Cup 1998 data (CUP), NHTSA crash statistics (FARS), the American Time Use Survey (ATUS) and the Integrated Health Interview Series (IHIS). They cover a wide spectrum, ranging from about 30k to 1.2M rows consisting of eight or nine quasi identifiers. The number of states in the generalization lattice, which is defined by the number of quasi identifiers as well as the height of the associated hierarchies, ranges from 12,960 for the ADULT dataset to 45,000 for the CUP dataset. The ADULT dataset serves as a de facto standard for the evaluation of anonymization algorithms.
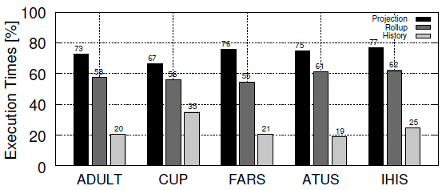
The benchmarks were performed on a commodity class Desktop machine equipped with a 4-core 3.1 GHz Intel Core i5 CPU with 6 MB cache and 8 GB of main memory running a 64-bit Linux 2.6.35 kernel and a 64-bit Oracle JVM in version 1.6.0 with a heap size of 512 MB.
The baseline of 100% is defined by the basic implementation, which does not include any optimizations. The optimizations are enabled incrementally and have a positive effect on the execution time for diverse datasets and configurations. When all optimizations are enabled the average execution time is reduced by a factor of about 4-5 for most datasets and about a factor of 3 for CUP.
It is important to note that even the basic implementation is highly efficient, as data is encoded and represented in a way that eliminates the need to apply complex join algorithms. When compared to other implementations, the ARX framework reduces execution times by up to multiple orders of magnitude.
Although the framework allows to efficiently implement well-known data anonymization algorithms, such as Incognito or Optimal Lattice Anonymization, it further provides a novel Algorithm that fully exploits the framework and its optimizations.