Help: Generalization Hierarchies

Creating generalization hierarchies (area 2)

ARX offers different methods for creating generalization hierarchies for different types of attributes. Generalization hierarchies created with the wizard are represented in a functional manner, meaning that they can be created for the entire domain of an attribute without explicitly addressing the specific values in a concrete dataset. This enables the handling of continuous variables. Moreover, hierarchy specifications can be imported and exported and they can thus reused for anonymizing different datasets with similar attributes. Please make sure that you first select an appropriate data type for the attribute. The wizard supports three different types of hierarchies:

1. Redaction-based hierarchies: this general-purpose mechanism allows creating hierarchies for a broad spectrum of attributes.
2. Interval-based hierarchies: these hierarchies can be applied to variables with a ratio scale.
3. Order-based hierarchies: this method an be used for variables with an ordinal scale.

Redaction-based hierarchies

Redaction is a highly flexible mechanism that can be applied to many attributes and is especially suitable for alphanumeric codes, such as zip codes or telephone numbers. The following image shows a screenshot of the respective wizard page:

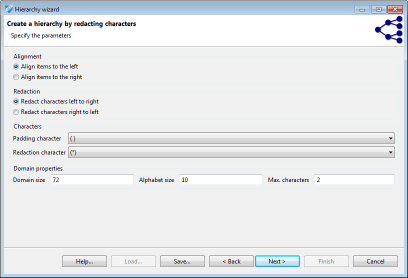
In ARX, redaction follows a two-step process. First, values are aligned either to the left or to the right. Then the characters are suppressed, again, either from left to right, or from right to left. All values are adjusted to a common length, by introducing padding characters. This character, as well as the character used for suppression can be specified by the user.

Interval-based hierarchies

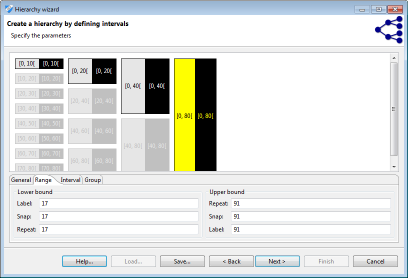
Intervals are a natural means of generalization for values with a ratio scale, such as integers, decimals or dates/timestamps. ARX offers a graphical editor for efficiently defining sets of intervals over the complete range of any of the above data types. As is shown in the following figure, first a sequence of intervals can be defined (shown on the left side of the figure). In the next step, subsequent levels consisting of groups can be defined. Each group combines a given number of elements from the previous level. Any sequence of intervals or groups is automatically repeated to cover the complete range of the attribute. For example, to generalize arbitrary integers into intervals of length 10, only one interval [0, 10] needs to be defined. Defining a group of size two on the next level, automatically generalizes integers into groups of size 20. As is shown in the image (W1), the editor visually indicates automatically created repetitions of intervals and groups.

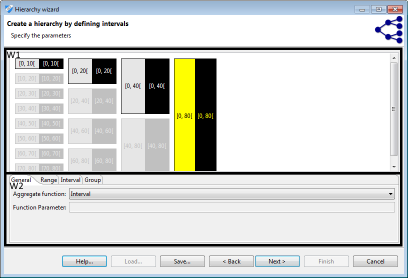
For creating transformation rules, each element is associated with an aggregate function (W2). These functions implement means for creating labels for intervals, groups and values that are to be translated into a common generalized value. In case of intervals, these functions are applied to the boundaries of each interval. Currently, the following aggregate functions are supported:

1. Set: a set-representation of input values is returned.
2. Prefix: a set of prefixes of the input values is returned. A parameter allows defining the length of these prefixes.
3. Common-prefix: returns the largest common prefix.
4. Bounds: returns the first and last elements of the set.
5. Interval: an interval between the minimal and maximal value is returned.
6. Constant: returns a predefined-constant value.

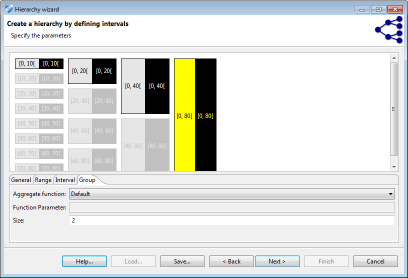
Clicking, on an interval or a group selects an editor that allows altering its further parameters. Elements can be removed, added and merged by right-clicking their graphical representation. Intervals are defined by a minimum (inclusive) and maximum (exclusive) boundary. Groups are defined by their size, as is shown in the following figure:

Interval-based hierarchies might define ranges in which they are to be applied. Any value out of the "label" range, will produce an error message. This can be used for sanity checks. Any value within the "snap" range, will be added to the first/last interval within the "repeat" range. Within this range, the sequences of intervals are groups will be repeated. The first and last intervals within the "repeat" range will be adjusted to cover the "snap" range.

Order-based hierarchies

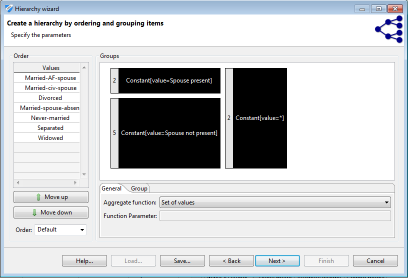
Order-based hierarchies follow a similar principle as interval-based hierarchies, but they can be applied to attributes with ordinal scale only. In addition to the types of attributes covered by interval-based hierarchies this includes strings, using their lexicographical order, and ordered strings. First, the attributes within the domain are ordered in a user-defined manner, or as defined by the data type. Second, the ordered values can be grouped using a mechanism similar to the one used for interval-based hierarchies. Note that order-based hierarchies are especially useful for ordered strings and therefore display the complete domain of an attribute instead of only the values contained in the concrete dataset. The mechanism can be used to create semantic hierarchies from a pre-defined meaningful ordering of the domain of a discrete variable. Subsequent generalizations of values from the domain can be labeled with user defined constants.

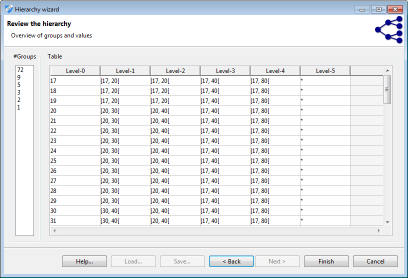
In a final step, all wizards show a tabular representation of the resulting hierarchy for the current input dataset. Additionally, the number of groups on each level is computed. The abstract specification created in the process can be exported and imported to allow reuse for different datasets with similar attributes.